The Remainder Theorem
Rule to remember:
- If a polynomial
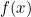 is divided by
is divided by 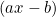 then the remainder is
then the remainder is 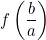 .
.
In the video tutorial I demonstrate this.
Finding the remainder when a cubic polynomial is divided by x+1
In the videos that follow, I run through some typical remainder theorem questions that you are likely to encounter. I start with this example.
Example in the video
- Find the remainder when
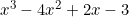 is divided by
is divided by 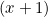
Finding the remainder when a quartic polynomial is divided by 2x-1
Example in the video
- Find the remainder when
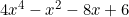 is divided by
is divided by 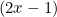
Finding constants in a polynomial given the remainders
Example in the video
- When
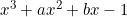 is divided by
is divided by  the remainder is 3 and when divided by
the remainder is 3 and when divided by 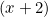 the remainder is -27. Find a and b.
the remainder is -27. Find a and b.



